Haskell入門

4. リストと再帰関数

関数型プログラミングの最も基本的なデータ構造であるリストについて学びます．リストは言語仕様で定義されている標準ライブラリの一部です．本章ではまず，標準ライブラリのAPIを調べる方法から学びます．その後，リスト処理に使われる代表的な関数を学びます．

4.1. どこで情報を得るか

プログラミング言語の学習では，言語仕様やライブラリの公式文書に慣れ親しむことも大切です．Haskellでライブラリの情報を得るにはHoogleで検索します．型やパッケージ，関数名で検索できます．入力フィールドの右側のドロップダウンメニューは，検索対象範囲を選択します．下図の「set:stackage」がデフォルトです．Stackageは，Hackageに登録されているライブラリの中で開発が続いているライブラリを集めたパッケージリポジトリです．基本的にはStackageに登録されているライブラリを使うのが無難なので，デフォルトのままで検索します．

パッケージとモジュール

大きなプログラムを作成するときには，複数のモジュールにソースコードを分割します．Haskellでは1つのファイルが1つのモジュールになります．複数モジュールを集めて，ライブラリやアプリケーションとしてアーカイブ化したものがパッケージです．

Haskellのパッケージを一元管理しているリポジトリがHackageです．Hackageの中で安定して開発されているものを集めたリポジトリがStackageです．ビルドツールのstackはStackageから依存ライブラリをダウンロードします．

Hackageに登録されているパッケージの検索ポータルがHoogleです．Googleをもじったのでしょう．ネーミングセンスが光ります．

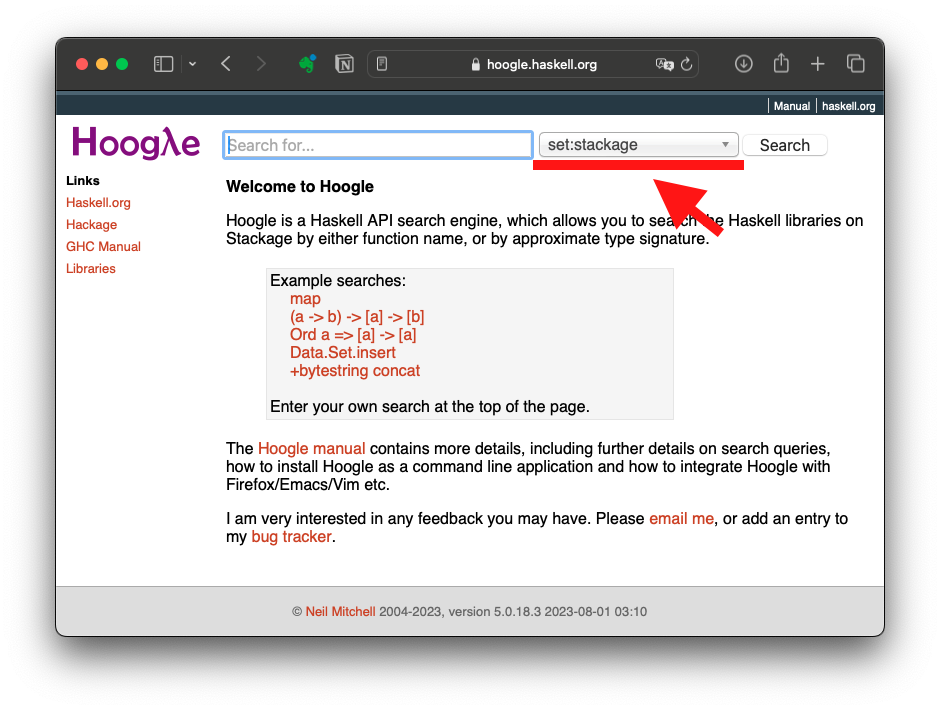
今回はリスト型なので[]で検索してみます．しかし[]では何も出てきません．そこでListで検索します．すると下図のようにトップ2つにmodule Data.Listが出てきます．モジュール名の下のbaseは，モジュールが入っているパッケージです．module Data.ListをクリックするとHackageのAPIドキュメントページに飛びます．HackageはHaskellのパッケージリポジトリで，あらゆるパッケージのダウンロードやAPIドキュメントを閲覧することができます．APIドキュメントにはソースコードへのリンクもあり，実際の定義を確認することができます．

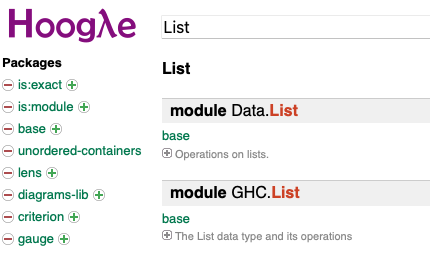
baseパッケージはHaskellの標準ライブラリなので，言語仕様を定めたHaskell ReportにもData.ListモジュールのAPIが載っています．Haskell Report 2010の第20章を参照してください．

どのプログラミング言語を使うにしても標準ライブラリに習熟することはとても重要です．Haskell Reportの第2部（第13章以降），もしくはHackageのbaseパッケージAPIは，機会あるごとに目を通すようにしましょう．

4.2. リストの作り方

これまでにリストリテラルを使ってリストを構築しました．リストの作成はリテラル表記以外に，range関数，cons関数，リスト内包表記の3つの方法があります．リスト内包表記は別の章に譲り，ここではrange関数とcons関数を使ったリスト作成方法を学びます．

4.2.1. range関数

range関数として知られる..演算子を使うと，指定した範囲のリストを作成できます．

[1 .. 10]        -- [1,2,3,4,5,6,7,8,9,10]
[1, 3 .. 10]     -- [1,3,5,7,9]

..演算子はEnum型クラスで定義されているenumFrom関数ファミリーの別名です．$[e_1 .. e_3]$はenumFromTo $\text{$e_1$ $e_3$}$と同じで，$[e_1,\, e_1 + 1,\, e_1 + 2,\, \cdots, \, e_3]$を生成します．

$ [e_1,\, e_2\, ..\, e_3] $はenumFromThenTo $\text{$e_1$ $e_2$ $e_3$}$と同じで， $ [e_1,\, e_1 + i,\, e_1 + 2i,\, \cdots, \, e_3] $を生成します．ただし$i = e_2 - e_1$です．つまり1番目と2番目の値の差を使った等差数列が作られます．2番目の値が1番目より小さければ，減少数列のリストが作られます．

もし，rangeの上界値を与えなかった場合は無限リストになります．ただし，IntのようにBounded型クラスのインスタンスの場合は，maxBoundまでの有限リストになります．ghci上で無限リストを評価すると，プロンプトが返らなくなります．その時はCtrl-Cで処理を中断できます．以下では，無限リストを作成して変数に格納し，最初の10要素だけ取り出しています．

ghci> let a = [1..]
ghci> take 10 a
[1,2,3,4,5,6,7,8,9,10]

[1..]を直接プロンプトに打ち込むと，無限リストを評価して画面に印字しようとするのでプロンプトが返らなくなりますが，上のように変数aに束縛した場合にはプロンプトが返ります．なぜなら，Haskellは遅延評価（lazy evaluation）といって，値が必要になるまで式を評価しないからです．上の1行目で無限リストを作成していますが，aには無限リストを生成する式だけが格納され，無限リストはまだ作られていません．2行目のtake 10 aで始めて必要な10要素だけ作成されます．遅延評価は??章で学びます．

4.2.2. cons関数

2項演算子:はリストのコンストラクタ（リストを生成する関数）でcons関数と呼ばれます．型は以下で与えられます．

(:) :: a -> [a] -> [a]

リストに入れたい要素を第1引数に与え，第2引数にリストを与えると，リストの先頭に要素を加えたリストを返します．

(:) 5 [1, 2, 3]    -- >  [5,1,2,3]  前置記法
5 : [1, 2, 3]      -- >  [5,1,2,3]  中置記法

上の例では第2引数に既存のリストがありますが，もし何もないところから5を要素とするリストを生成するには第2引数に空リスト（null list）[]を与えます．空リスト[]はnilとも呼ばれます．

(:) 5 []    -- >  [5]  前置記法
5 : []      -- >  [5]  中置記法

consを連続して呼び出すことで[1, 2, 3, 4]が構築できます．

1 : 2 : 3 : 4 : []    -- >  [1,2,3,4]

「:」演算子は右結合なので，上のコードは以下と同じです．

1 : (2 : (3 : (4 : [])))    -- >  [1,2,3,4]

中置演算子の結合規則と優先順位は，ghciの:infoコマンドで確認できます．

ghci> :info (:)
type [] :: * -> *
data [] a = ... | a : [a]
        -- Defined in ‘GHC.Types’
infixr 5 :

上の出力の最終行のinfixr 5が結合規則と優先順位を表します．infixは中置演算子であることを，その後のrは右結合であることを意味します．最後の5は優先順位を表します．この値が大きいほど優先順位が高く，0から9までの値が割り振られます．結合性の指定がない場合はデフォルトで左結合になります．

4.3. 複合的なリスト

多次元のリストを作りたい場合，リストの要素にリストを作れます．ただし，リストは同じ型の要素しか持てないため，内部の要素も全てリストでなければなりません．内部のリストの長さが異なっていても型は同じなので問題ありません．

[1, 2, [3, 4], 5, 6]       -- >  エラー，[Int]型のリストに[[Int]]が含まれている
[[1, 2], [3, 4, 5], [6]]   -- >  長さが異なっていても型は[[Int]]なのでOK

同様に，タプルや関数を内部に含むこともできます．

[(1,"Tokyo"),(2,"Osaka"),(3,"Nagaya")]    -- >  型: Num a => [(a, String)]
xs = [(*), (+), (-)]                      -- >  型: Num a => [a -> a -> a]

ghciに関数のリストを直接入力すると，リストを画面に印字しようとしてエラーになります．関数を文字列として印字する方法がないからです．上の例の2行目のように変数に代入すると，:typeコマンドでxsの型を調べられます．

4.4. リスト処理

4.4.1. headとtail

head関数はリストの先頭要素を返し，tail関数は先頭要素を除いた残りのリストを返します．

head [1, 2, 3, 4]    -- >  1
tail [1, 2, 3, 4]    -- >  [2, 3, 4]

4.4.2. lengthと要素へのアクセス

リストの長さを得るにはlength関数を使います．

length [1, 3, 5, 7]                -- >  4
length [[1], [2,3,4,5,6], []]      -- >  3

リストのインデックス番号でアクセスするには!!演算子を使います．インデックス番号は0スタートです．リストの範囲外のインデックスにアクセスすると例外（exception）が投げられます．「例外」はプログラム内部で異常を知らせるメカニズムです．例外とエラー処理については別の章で学びます．

[1, 2, 3, 4] !! 0    -- >  1
[1, 2, 3, 4] !! 1    -- >  2
[1, 2, 3, 4] !! 4    -- >  例外（exception）が投げられる

リストはメモリ上でコンスセル（cons cell）と呼ばれるセル（cell）の繋がりで出来ています．例えば，4つの要素を持つリスト[1, 2, 3, 4]は4つのコンスセルが以下のように繋がってできています．図中の4つの長方形がコンスセルです．

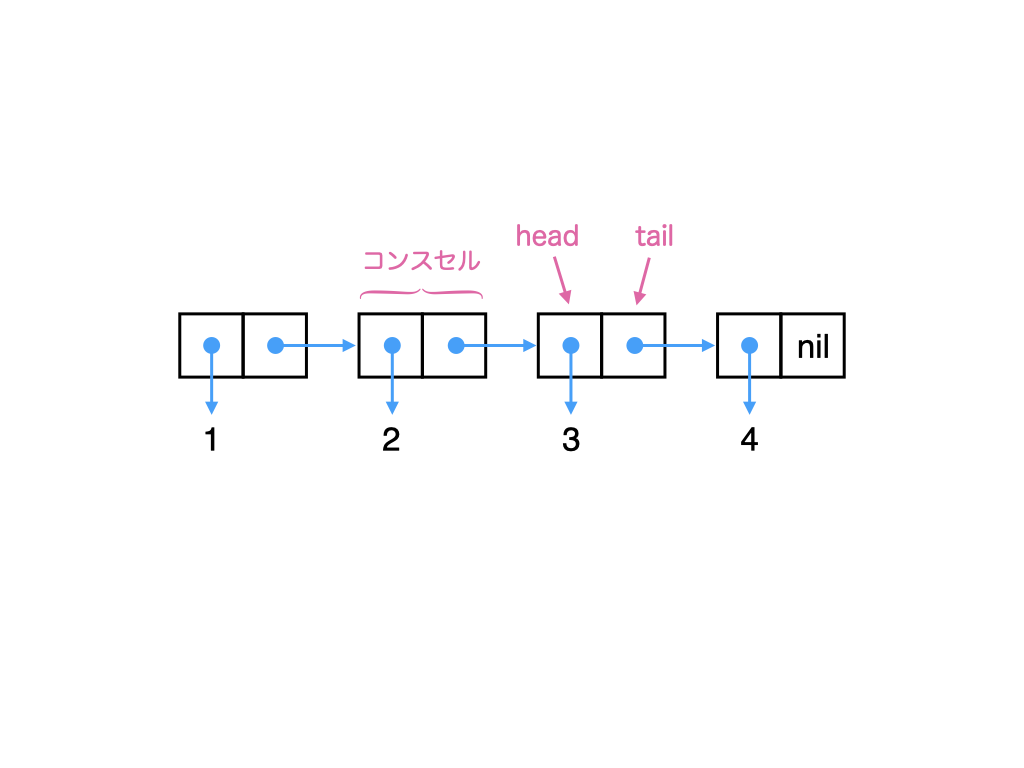
cons cells

各コンスセルはheadとtailの2つの部分からできています．各コンスセルのtail部分には次のコンスセルへのポインタが格納されています．ポインタとはメモリ上のアドレス値のことです．ポインタにアクセスすることで，ポインタ（アドレス値）が指し示す先にあるデータにアクセスできます．図の矢印の始点に描かれている丸印がポインタ（アドレス値）を表していて，矢印がポインタが指し示す先を表しています．

xs = [1, 2, 3, 4]が評価されると，リスト先頭要素のhead部分を指し示すポインタが，変数xsに代入されます．xs !! 3を実行すると，4番目の要素にアクセスするために，xsに束縛されている先頭要素からポインタをたどっていかなければなりません．同様の理由で，length関数がリストの長さを得るには，先頭から全てのコンスセルをたどって最後のnilにたどり着くまでカウントしなければなりません．

したがって，length関数と!!演算子の実行時間はリストの長さに比例します．要素数nに比例して実行時間が増加する計算時間を$O(n)$と書きます．lengthと!!の計算時間は$O(n)$です．

4.5. 再帰関数とリスト処理

よく使うリスト処理の関数はまだあるのですが，それらをダラダラと説明しても面白味に欠けるので，標準ライブラリに用意されている関数と同じものを，自分で作ってみましょう．

関数の定義の仕方はSection 2.4とSection 3.9で学びました．リストを引数に取り，その長さを返すmyLength関数は以下のように書けます．

myLength :: [a] -> Int        (1)
myLength xs = length xs       (2)

1	任意の型の要素を持つリストを引数に取り，リストの長さを整数で返す関数の型．
2	引数を`xs`に束縛し，標準ライブラリの`length`関数を使って長さを返す．

上の関数は標準ライブラリを使って長さを求めています．この後これを自分で実装します．リストのように複数のデータを内部に持つデータ型をコンテナ（container）とかコレクション（collection）と呼びます．こうしたオブジェクト^[2]を引数にとる場合，複数形を意識して引数名にsを付ける慣習があります．

リスト処理では再帰（recursion）という手法を使います．再帰とは自分で自分を呼び出すことです．数学の階乗の定義が再帰を使っています．

0! = 1
n! = n (n - 1)!

上の2行目を見ると，左辺の$n!$を定義する右辺で，再び階乗記号を使っておりトートロジーになっています．つまり，階乗記号!を使って!を定義しています．しかし，皆さんご存知のように，いかなる整数$n$でも順に展開していけば，やがて1行目の定義$0! = 1$にたどり着き，そこからドミノ倒しで$n \times (n-1)(n-2) \cdots 1$を得ます．

プログラミングでもこのように関数定義内で自分自身を呼び出すことで関数を定義することができます．階乗を計算するfactorial関数は以下のように定義できます．

factorial :: Int -> Int
factorial n = if n == 0 then 1 else factorial (n - 1)

ここからは複数行にまたがる関数を定義していくので，コードはソースファイルに書きましょう．この章ではData.Listモジュールで定義されている関数を使うのでソースファイルの冒頭にimport Data.Listを記入してください．

例えばimport文と上の2行をch04-list.hsファイルに書きます．そして，ghciから:load ch04-list.hsでロードします．ファイルを編集したら次からはファイル名なしで:reloadもしくは:rを実行することで再ロードできます．

上のファイルをロードしてfactorial 10をghciで実行すると3628800を得るはずです．

上の定義ではif式を使いました．if式はif 条件 then 式1 else 式2の書式で，「条件」がTrueなら「式1」の評価結果が返り，Falseなら「式2」の評価結果が返ります．下のように複数行に書くこともできます．その場合は，意味のあるブロックでインデントを揃えなければなりません．

factorial :: Int -> Int
factorial n =
  if n == 0
    then 1
    else n * factorial (n - 1)

nが0のケースは1を返し，それ以外ならn * factorial (n - 1)を返すという定義は，数学の階乗の定義そのものです．もし，nが0のケースを書かなかったら，上の関数は永遠にnを1だけデクリメントしながら自分自身を呼び続けて無限ループになります．n == 0のケースが終端条件（terminal condition），もしくはベースケース（base case）になっています．

Haskellの関数定義では，ケース分けをif式ではなく，ケース毎に関数定義を列挙して書くことができます．むしろ列挙する書き方の方が一般的です．以下では関数名にプライムを付けて新たにfactorial'関数をケース分けで定義しています．ghciにリロードして同じ結果が得られるか確認しましょう．

factorial' :: Int -> Int
factorial' 0 = 1                         (1)
factorial' n = n * factorial' (n - 1)    (2)

1	`n`が`0`のケースの関数定義．
2	`0`以外の`Int`の値のケース．

ループと再帰

他の言語にはループ処理を書くためのfor文やwhile文が用意されていますが，Haskellにはありません．Haskellでループ処理をするには再帰関数を用います．

純粋関数型言語であるHaskellには，値を返さない「文（ステートメント）」がそもそも有りません．したがってfor文やwhile文もありません．もちろん，forループの最後の処理を値として返せばfor式になりますが，forループやwhileループでは値が変化するカウンタ変数が必要です．Haskellは変数の書き換えを許さないので，結局再帰を使うしかありません．

あらゆるループ処理で再帰を用いるので，再帰関数はしっかり身につけましょう．

4.6. パターンマッチ

関数定義は引数のパターンに応じて分けて書くことができます．関数の引数部分にパターンを記述すると，上から順にパターンと照合され，最初にマッチした定義が関数本体として実行されます．

関数が呼び出されると上から順にパターンと引数が照合され，最初にマッチした定義が実行される．

関数名 パターン1 = 定義1
関数名 パターン2 = 定義2
         ⋮
関数名 パターンn = 定義n

4.6.1. 値のマッチ

パターン部分がリテラル値の場合は，引数 == リテラル値がTrueのときパターンにマッチします．

isDogOrCat :: String -> String
isDogOrCat "meow" = "It's a cat!"      (1)
isDogOrCat "bow"  = "It's a dog!"      (2)
isDogOrCat sound  = "I don't know!"    (3)

1	`isDogOrCat "meow"`と呼び出された時に引数がマッチして実行される．
2	`isDogOrCat "bow"`と呼び出された時に引数がマッチして実行される．
3	上記以外の引数が与えられた時に実行される．これはパターン部分が名前（変数）のケースで，次節で解説．

4.6.2. 名前（変数）のマッチ

パターン部分が名前（変数）のときは，いかなる引数にもマッチします．前節最後のコードでisDogOrCatの3番目の定義の引数はsoundでした．これは名前（変数）なので，いかなる値にもマッチします．

よくある間違いは，下の例のように関数外部で変数showNameに値を設定していて，その値とマッチさせるためにパターンにshowNameと書いてしまうケースです．パターン部分のshowNameは関数の引数を受け取るパラメータ変数で，関数の外で定義された変数showNameとは別物です．この場合，パターン部分のshowNameはどんな値にもマッチします．

showName = True                          (1)

hello :: Bool -> String -> String
hello showName name = "Hello, " ++ name  (2)
hello False    name = "Hello!"           (3)

1	トップレベルで定義された`showName`変数．
2	この`showName`は引数を受け取るパラメータ変数で，トップレベルの`showName`とは別物．変数なのでどのような値の引数にもマッチする．
3	このコードが実行されることはない．

上のコードは，hello True Hanakoと関数が呼び出されたとき，第1引数のTrueを関数外部で定義したshowName変数の値にマッチさせようとしています．しかし，パターン部の変数は全ての値にマッチするため，たとえ，hello False Hanakoと呼び出しても1つ目の定義が実行されます．2番目の定義が実行されることはありません．

4.6.3. コンストラクタを含むパターンのマッチ

パターン部分がデータのコンストラクタを使って記述されている場合，データの構造が同じならばマッチします．例えばリストの:演算子と[]は，それぞれコンスセルとnilを生成するコンストラクタです．これを用いて以下のように書くとheadとtailから成るリストにマッチします．

list2pair :: [Int] -> (Int, [Int])
list2pair (x:xs) = (x, xs)         (1)

1	パターン部分を括弧で囲まないと関数の左結合が優先されて`list2pair`と`x`が結合してしまう．

上の引数部分はリストのコンストラクタ:を使ってheadとtail部分からなるリスト構造を表しています，したがって，headとtailを持ついかなる整数リストにもマッチします．マッチした際，xには引数のhead部分が，xsにはtail部分がそれぞれ束縛されます．以下のコードは，上で定義したlist2pairの呼び出し例です．

list2pair [1..5]    -- >  x=1, xs=[2,3,4,5] にマッチ
list2pair [1]       -- >  x=1, xs=[] にマッチ        (1)
list2pair []        -- >  例外が投げられる            (2)

1	1要素のリストでもコンスセルにはhead部分とtail部分がある．ただしtail部分は`nil`，すなわち空リスト．
2	`[]`すなわちnilはコンスセルではないので，head部分とtail部分の構成になっていない．したがって，`(x:xs)`にはマッチせずエラーとなる．

上の3つの関数呼び出しで分かるように，list2pairには空リストが与えられた場合の定義がありません．このように一部の引数に対してしか定義されていない関数を部分関数（partial function）と呼びます．それに対して全ての引数に対して定義されている関数は全域関数（total function）と呼びます．

以下のように，list2pairの定義に空リストのケースを加えれば全域関数になります．

list2pair' :: [Int] -> (Int, [Int])
list2pair' (x:xs) = (x, xs)
list2pair' [] = (minBound, [])          (1)

1	`(Int, [Int])`型を返さなければならないので，空リストが与えられた場合は，`Int`型の最小値と空リストのペアを返すことで，異常値が引数に与えられたことを示している．

リストはcons関数:を用いてもっと複雑な構造にもマッチさせることができます．以下，いくつか例を示します．

引数                 パターン          マッチした結果
[1,2,3]             [a, b, c]        a=1, b=2, c=3
[1,2,3,4,5]         a : b : xs       a=1, b=2, xs=[3,4,5]
[[1,2,3], [4, 5]]   [a:xs, [b, c]]   a=1, b=4, c=5, xs=[2,3]

リテラルの[a, b, c]は，a : b : c : []のシンタックスシュガー（構文糖衣）なので，コンストラクタを用いて記述したパターンと同じように機能します．

上のパターンマッチを確認したい場合は，ghciで以下のように実行します．

ghci> let [a:xs, [b, c]] = [[1,2,3], [4, 5]]
ghci> a
1
ghci> b
4
ghci> c
5
ghci> xs
[2,3]

本章はリストの章なのでリストを中心に説明しましたが，タプルでもパターンマッチは使えます，タプルの括弧がコンストラクタの役割を果たすので，パターンマッチを用いて以下のようにタプルの中身を取り出すこともできます．

let (a, b, c) = (1, 2, 3)    -- >  a=1, b=2, c=3

パターンマッチは，関数定義以外の場所でも使えます．上の例では変数に値を束縛する際に使いました．他にも，これから学ぶ局所変数の作成時やリスト内包表記などさまざまな場面で使うことができます．

4.6.4. ワイルドカード

何にでもマッチするけど値は必要ないというケースもあります．アンダースコア記号_はこのようなケースに使い，ワイルドカードと呼ばれます．例えば以下のdropTwo関数は，リストの先頭要素2つを破棄した残りをリストとして返す関数を定義しています．

dropTwo :: [a] -> [a]
dropTwo (_ : _ : xs) = xs   (1)

dropTwo [1..10]    -- >  [3,4,5,6,7,8,9,10]

1	先頭2要素は不要だが，パターンにはマッチさせたいのでワイルドカードを使っている．

4.7. length関数の自作

それでは今学んだ再帰とパターンマッチを用いてlength関数を自作してみましょう，リストの長さは「headの長さ + tailの長さ」であることに注意すると，以下のロジックで求めることができます．

空リストなら長さは0．
それ以外のリストの長さは，headを除いたリスト（tail部分）の長さを求めた結果に1加える．

後半の「headを除いたリストの長さ」を求めるときに自分自身を呼び出す再帰を使います．

myLength :: [a] -> Int
myLength [] = 0
myLength (x:xs) = 1 + myLength xs  (1)

1	右辺は「`x`の長さ + `xs`の長さ」です．

以下が実行結果です．

ghci> myLength [1..9]
9
ghci> myLength "This is a pen"
13

末尾再帰最適化（tail call optimization）

他のプログラミング言語を学んだことがある人は，末尾再帰にしなくて良いのかと心配されるかもしれません．遅延評価を特徴とするHaskellでは末尾再帰であろうがなかろうが，メモリ使用量に差は出ません．つまりスタックオーバーフローになるか否かとは関係ないということです．むしろ遅延評価によるサンクと呼ばれるプロミスオブジェクトが占有するメモリが問題になります．

メモリ使用量は末尾再帰とあまり関係しませんが，GHCは末尾再帰最適化を行います．再帰関数はループに変換され関数呼び出しがなくなるため，実行効率は良くなります．末尾再帰と遅延評価については後の章で学びます．

4.8. dropとtake

dropとtake関数はとてもよく使います．drop n xsはリストxsの先頭からn個の要素を取り除いたリストを返します．take n xsはリストxsの先頭からn個の要素を取り出してリストにして返します．与えられたリストの範囲を超える要素を取り出したり，取り除いた場合には，リストの要素数を上限にして結果が返ります．

drop 4 ['a' .. 'z']    -- >  "efghijklmnopqrstuvwxyz"
drop 4 "abc"           -- >  ""
drop 4 []              -- >  []

take 4 ['a' .. 'z']    -- >  "abcd"
take 4 "abc"           -- >  "abc"
take 4 []              -- >  []

例題

dropとtakeを再帰を使って実装しなさい．

実装例（クリックすると開きます）

ghciでdropの型を調べてその型に合わせます．空リストが与えらえた場合は，第1引数に関係なく空リストを返すので，ワイルドカードが使われています．

drop' :: Int -> [a] -> [a]
drop' _ [] = []
drop' 0 xs = xs
drop' n (x : xs) = drop (n - 1) xs

以下はtakeの実装です．ワイルドカードが２箇所で使われています．

take' :: Int -> [a] -> [a]
take' _ [] = []
take' 0 _ = []
take' n (x : xs) = x : take' (n - 1) xs

4.9. アペンド

すでに何度も出てきた++演算子はリストの後ろに別のリストをアペンドします．例えば，以下の処理がメモリ内でどのようになっているか考えてみましょう．

x = [1,2,3]
y = [4,5,6]
z = x ++ y     -- >  [1,2,3,4,5,6]

仮にxが指し示すリストの後ろにyをそのまま連結してzを構築したとしましょう．そうすると，xの中身はzと同じ[1,2,3,4,5,6]に変わってしまいます．Haskellでは値の変更が出来ないので，xの最後のコンスセルのtail部分のポインタを書き換えることは実際にはできません．したがって，このような連結は出来ません．

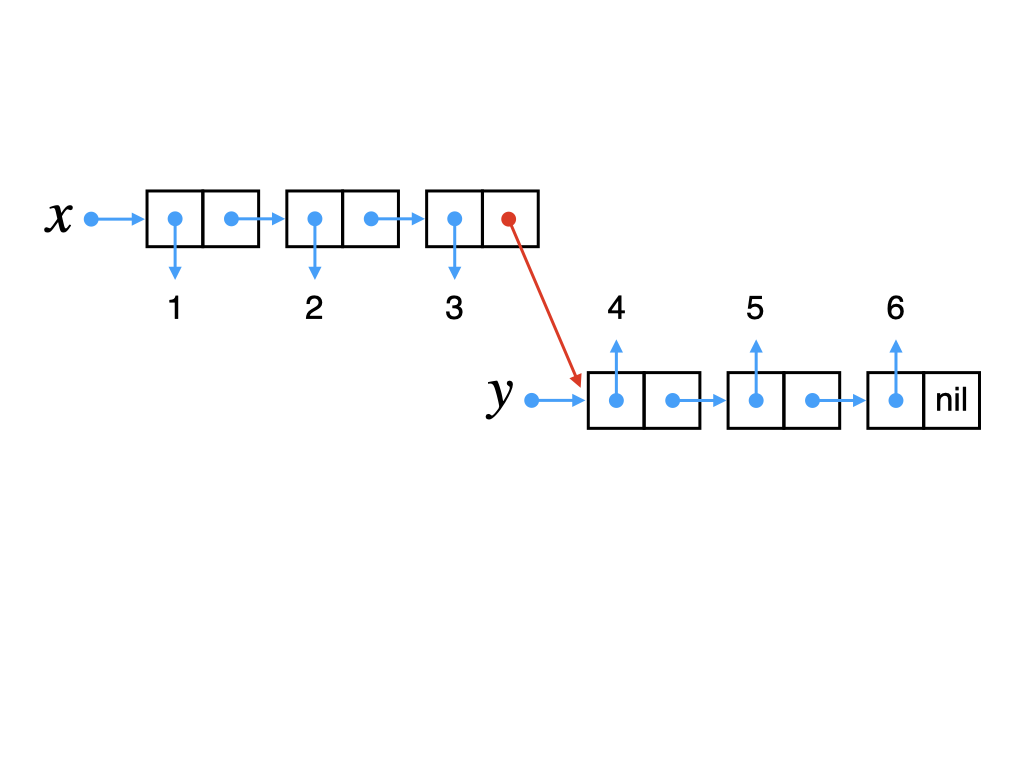
append wrong

アペンド処理は以下のようにxを複製し，その後ろにyを連結します．こうすると，xもyも元のリストを指し示したまま変化しません．さらに，zの後半部分のデータはyと共有されるのでメモリも節約できます．また，xを複製する際は，コンスセルのみ新たに作成してデータはx内のものを使うので，xのデータもzと共有されます．

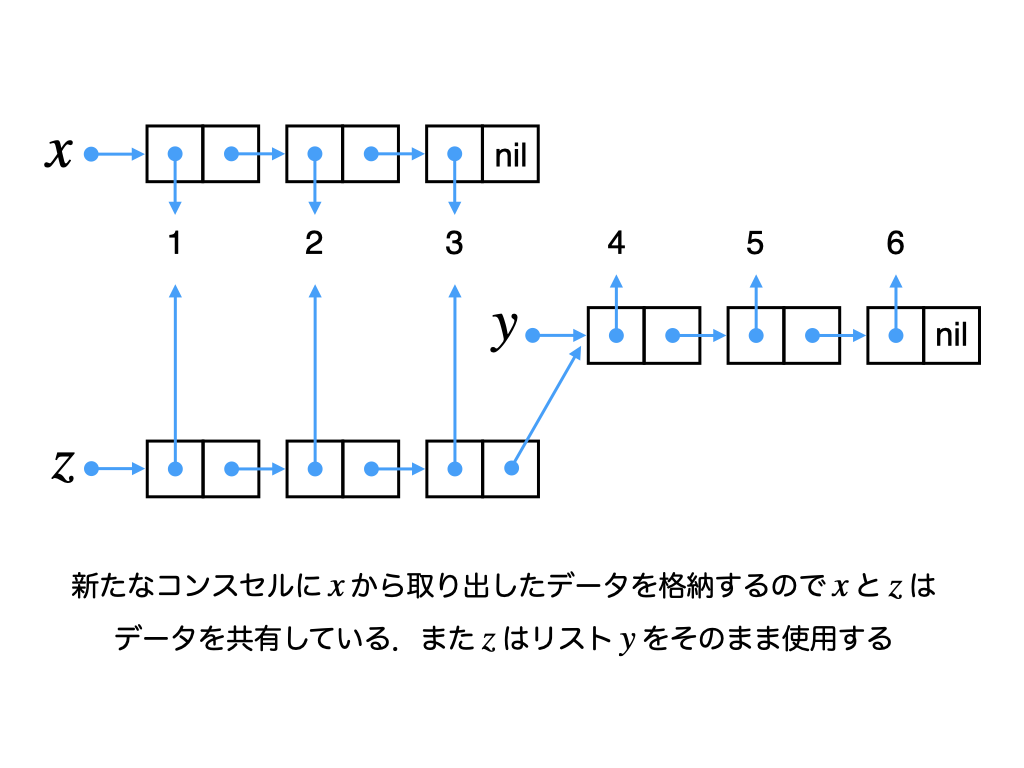
append correct

アペンド処理は，第1引数の要素全てをトラバースして複製しなければならないので，処理時間は$O(n)$になります．特に第1引数がとても長く，後ろに短い要素から成るリストを繰り返し追加したい場合には，リストではなく他のデータ構造を使うことを考えましょう．もしくは，reverse関数で先頭リストを逆順にし，そのリストの頭に要素をconsしていき，一連の追加処理が終わったら再びreverseして元に戻すのが良いでしょう．

ディープコピーとシャローコピー

データを保持するコンスセルのみ複製して，中身のデータは複製しないコピー方法をシャローコピー（shallow copy）といいます．上の図のzはxのシャローコピーです．関数型プログラミングではデータの中身を書き換えないので，他の変数と安全にデータを共有することができます．これにより，メモリだけでなく，コピー時間も短縮できます．変数を書き換えるオブジェクト指向プログラミングでは，ディープコピーをしないとバグの原因になることがあります，

例題

第1引数のリストの先頭要素を，「第2引数にアペンド済みのリスト」とconsすることで，++を実装しなさい．「第2引数にアペンド済みのリスト」の部分が再帰になります．

実装例（クリックすると開きます）

ghciで型を調べると(++) :: [a] → [a] → [a]を得ます．ここではappendという関数名で実装します．

append' :: [a] -> [a] -> [a]
append' [] xs = xs
append' (x : xs) ys = x : (append' xs ys)

ちなみに，:演算子の優先順位は通常の関数の優先順位より低いので，最後の行の右辺の括弧は冗長になります．

4.10. reverse

reverse関数はリストの順番を反転させます．

reverse [1..10]    -- >  [10,9,8,7,6,5,4,3,2,1]

リストを再帰的に反転させるには，先頭要素を取り出し，残りを反転させ，その後ろに先頭要素をアペンドすることで実現できます．アペンド演算子++は2つの「リスト」を接続することに注意すると以下のように定義できます．

reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x : xs) = reverse' xs ++ [x]  (1)

1	head部の`x`をアペンドする際，リストにする必要がある．

どのような処理が行われるかreverse' [1,2,3,4]を右辺の定義に置き換えて展開してみましょう．

コード 3. アペンドを用いたreverseの展開

reverse' [1,2,3,4] = reverse' [2,3,4] ++ [1]
                   = (reverse' [3,4] ++ [2]) ++ [1]
                   = ((reverse' [4] ++ [3]) ++ [2]) ++ [1]
                   = (((reverse' [] ++ [4]) ++ [3]) ++ [2]) ++ [1]
                   = ((([] ++ [4]) ++ [3]) ++ [2]) ++ [1]
                   = (([4] ++ [3]) ++ [2]) ++ [1]      (1)
                   = ((4 : [] ++ [3]) ++ [2]) ++ [1]   (2)
                   = ((4 : [3]) ++ [2]) ++ [1]
                   = ([4,3] ++ [2]) ++ [1]             (3)
                   = (4 : [3] ++ [2]) ++ [1]
                   = (4 : 3 : [] ++ [2]) ++ [1]
                   = (4 : 3 : [2]) ++ [1]
                   = [4,3,2] ++ [1]                    (4)
                   = 4 : [3,2] ++ [1]
                   = 4 : 3 : [2] ++ [1]
                   = 4 : 3 : ([] ++ [2]) ++ [1]
                   = 4 : 3 : [2] ++ [1]
                   = 4 : 3 : 2 : [] ++ [1]
                   = 4 : 3 : 2 : [1]
                   = [4,3,2,1]

1	前節の`append' [] xs`の定義を適用して`[4]`に`[3]`のアペンド処理開始．
2	前節の`append' (x : xs) ys = x : (append' xs ys)`を適用．
3	前節の`append`を用いて`[4,3]`に`[2]`をアペンドする処理を開始．
4	前節の`append`を用いて`[4,3,2]`に`[1]`をアペンドする処理を開始．

定義を置き換えていくと，reverse'の再帰処理中に作られるサブリストを繋げるために，++演算子，すなわちappend'の再帰処理がサブリスト毎に発生するのがわかります．そこで++を使わずにreverseさせる方法を考えます．

リストを反転させるには，反転済みのリストの前に，反転したいリストのheadをconsすれば良いわけです．そこで，反転したいリストと反転済みのリストの2つを引数に取る再帰関数を補助関数として作成します．

reverseHelper :: [a] -> [a] -> [a]
reverseHelper [] accum = accum
reverseHelper (x : xs) accum = reverseHelper xs (x : accum)

reverseHelper関数の第1引数は，これから反転しようとしているリストです．第2引数のaccumは，反転済みの結果を保存するために使います．再帰呼び出しをしながら，処理結果を引数に蓄積していきます．このように処理結果を蓄積していく変数をアキュムレーター（蓄積器）と呼びます．アキュムレーターを使った再帰については末尾再帰の章で詳しく学びます．

最初の段階では反転処理結果が何も無いので，アキュムレーターは空リストになります．したがってreverseHelperの第2引数に空リストを渡して以下のように呼びだせばリストを反転できます．

ghci> reverseHelper [1,2,3,4] []
[4,3,2,1]

この補助関数を用いるとreverse関数を以下のように定義できます．

コード 4. アペンドを使わないreverseの定義

reverse'' :: [a] -> [a]
reverse'' x = reverseHelper x []

4.11. 本章のまとめ

ライブラリや関数に関する公式文書の見つけ方を学びました．Hoogle，Stackage，Hackageの役割を学びました．
関数型プログラミングの基本ツールであるリストの生成方法としてrangeとcons関数:を学びました．
リストのメモリ内構造を学びました．
標準ライブラリで用意されているリスト処理関数のうち，head，tail，length，drop，take，++，reverseの使い方を学ぶと同時に，自分で同じ機能を再帰を用いて実装しました．
パターンマッチを用いた関数定義の方法を学びました．

以下の練習問題ではさらにlast，init，zip，intersperse関数の使い方と実装を学ぶので必ず解きましょう．

4.12. 練習問題

コード 4で定義したreverse''をコード 3のように展開しなさい．そして計算時間が要素数に比例することを確認しなさい．
Data.Listモジュールで定義されているlast関数の動作をAPIドキュメントで調べ，再帰を用いて実装しなさい．ただし，last関数の型に付いている型クラス制約は無視し，[a] → aの型で定義しなさい．
同じくData.Listモジュールのinit関数の動作をAPIドキュメントで調べ，再帰を用いて実装しなさい．ただし，init関数の型に付いている型クラス制約は無視し，[a] → [a]の型で定義しなさい．
同じくzip関数の動作をAPIドキュメントで調べ，再帰を用いて実装しなさい．

2. オブジェクトとは，メモリ内に実体を持つデータのことを指します．慣れないうちは単にデータと読み替えてもらって構いません．